AVL树(Adelson-Velsky and Landis Tree),是一种自平衡二叉查找树。网上的介绍比较多,这里仅作为学习记录。
老规矩,代码实现直接跳转至最后一章。
1. 二叉查找树
下面这个树就是二叉查找树,可以看到。每个节点的左子节点,要小于自己。右子节点,要大于自己。
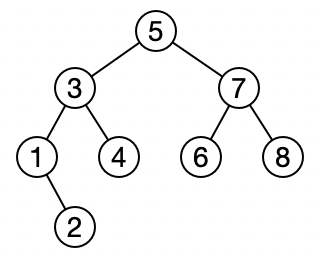
所以总的来说,二叉查找树,是一种有序的二叉树。同时正因为这种有序的特性,使得进行查找时效率,类似于二分法查找,会远高于依次遍历。
但二叉查找树的高效率是存在缺陷的。举个例子,我们继续向刚才的树里依次插入一些数据:9、10、 11,那树就变成了这个样子:
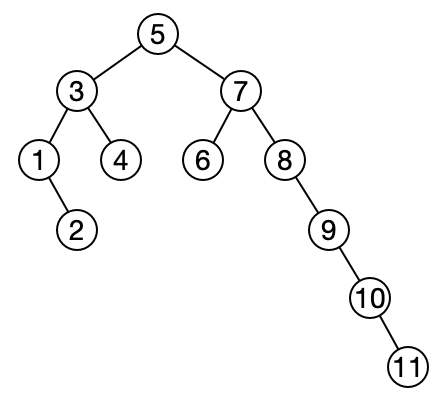
此时如果我们想要查找11的话,因为右侧分支处于线性的结构,所以查找效率等同于遍历。甚至于更为极端的例子,使用1、2、3、4、5、6这样的数据,来构造二叉查找树的话,得到的整棵树都是线性的结构:
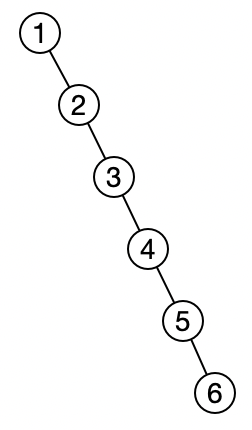
2. AVL树
AVL树和二叉查找树的区别,就在于AVL树具有自平衡的特性。先不管什么叫自平衡,而是先关注其作用。
自平衡特性的作用,就在于阻止线性结构的产生,从而避免查找效率的遍历化倾向。
自平衡的定义有很多种,对于红黑树、AVL树、Treap树而言都各不相同,用以满足各自的算法逻辑。在AVL树中,平衡的定义,指的是每个节点的左子树深度,和右子树深度的差值,不大于1。举几个例子:
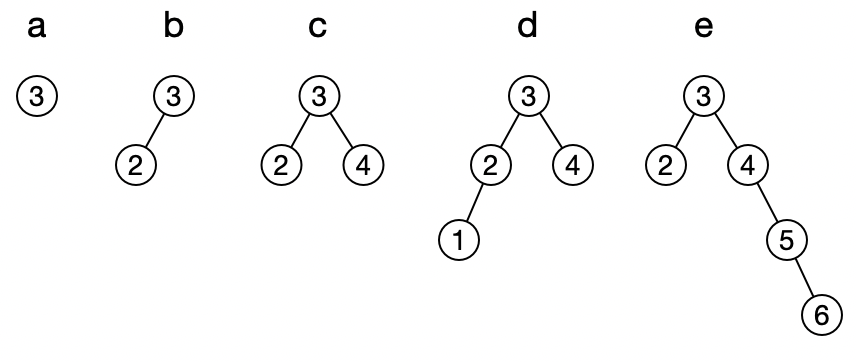
上面的五个树中,前四个都是平衡的。最后一个树中,节点4的左子树深度是0,右子树深度是2,相差大于1,所以是不平衡的。同时这个树中的节点3,左右子树深度差也是大于1的。
而自平衡中的“自”,指的就是对树进行插入、删除节点操作之后,还能自动调整保持平衡。
2.1 插入操作
AVL树的插入操作分为两步,第一步跟二叉查找树一样,把节点按大小顺序插入到树中即可。第二步则是检查平衡性,如果不平衡的话,就进行调整达到平衡。所以在这里,我们只关注如何进行平衡性的调整。
用下面这个树作为例子:
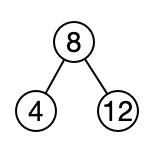
然后向其中插入数据,树结构变成下面这四种不平衡的状态:
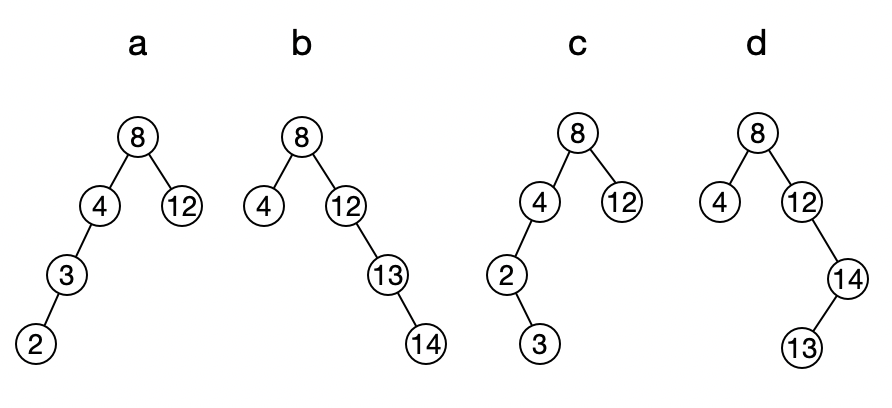
对于a、b两种情况,只要把导致不平衡的最小子树集合,进行适当旋转即可重新达到平衡状态:
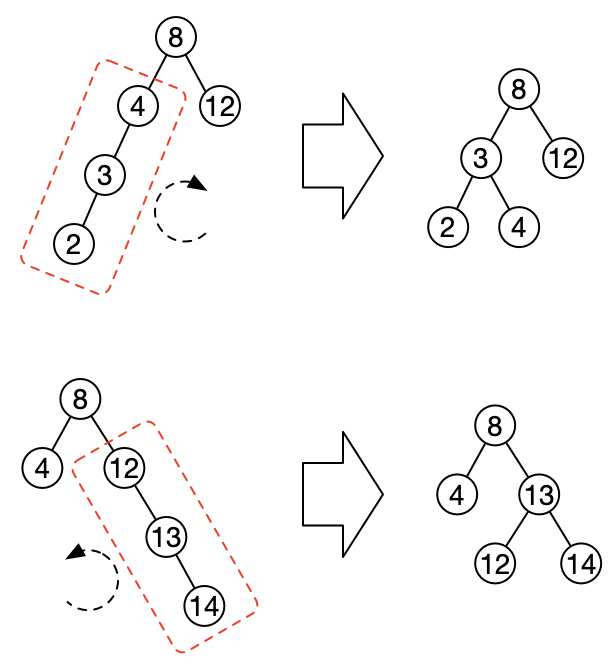
而c、d这两种不平衡最小子树方向不一致的情况,就先把方向旋转成一致的,再按照a、b的情况处理就好了:
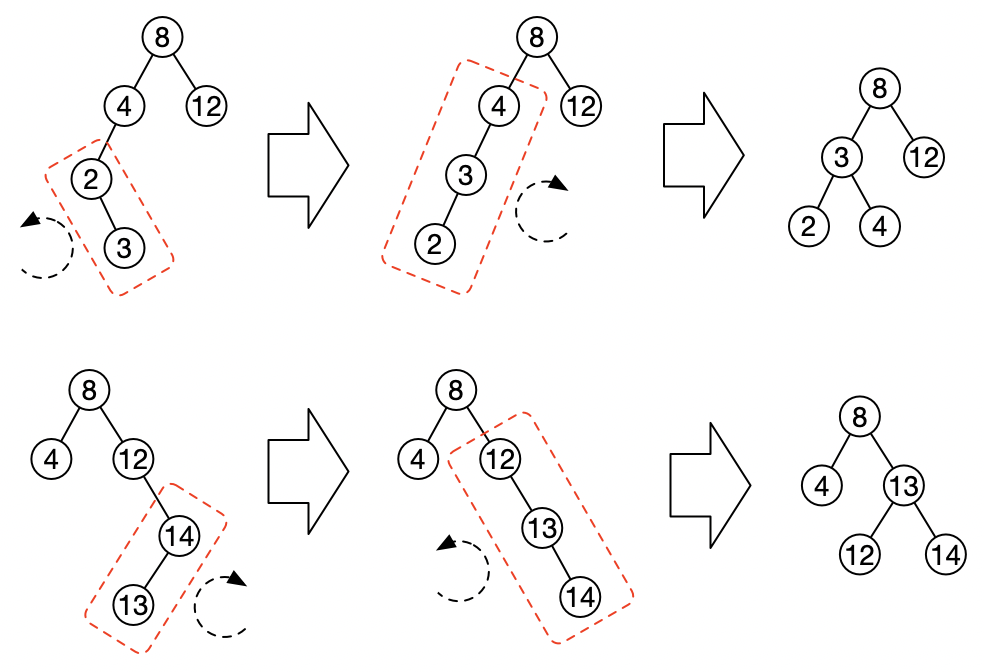
当然,除去上面几种简单的情况外。在比较复杂的情况下,被旋转节点左右子树,还包含有子树时,就得在旋转之前,多一个步骤。用下面的树举例子:
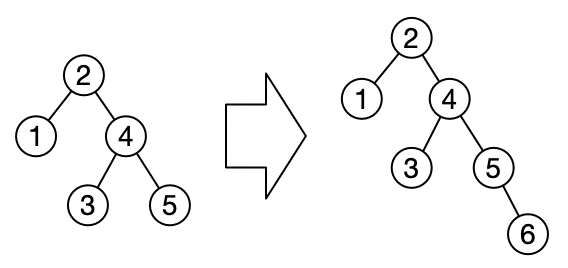
左边是原本已处于平衡态的树结构,右边是向其中插入节点6后,处于非平衡态的树结构。
此时,节点2的左右子树深度差大于1,需要进行旋转操作恢复平衡。但因为其右子节点4,还有着自己的子树结构,所以进行下面的步骤恢复平衡:
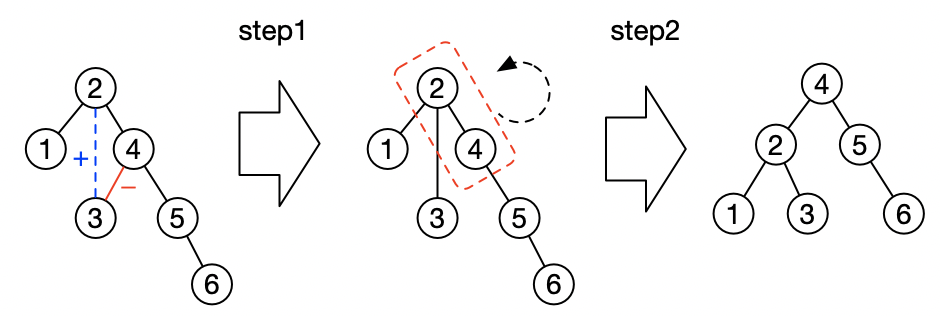
- 1)step1:找到节点
2右子节点的左子节点,并将其设为节点2的右子节点。 - 2)step2:进行旋转操作恢复平衡性
上面的例子,是右子树深度大于左子树深度,且右子节点还包含有子树时的情况。
如果反过来,是左子树深度大于右子树深度,且左子节点还包含有子树时的情况。那就相应的反过来,先构建和左子节点的右子节点的关联,然后再进行旋转即可:
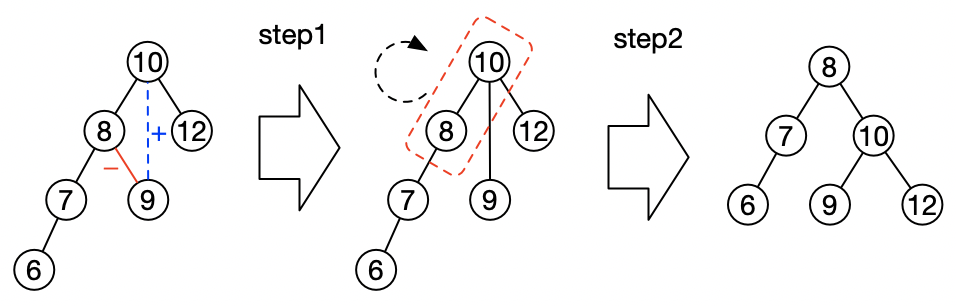
2.2 删除操作
AVL树的删除操作比较简单。以下面的树作为例子:
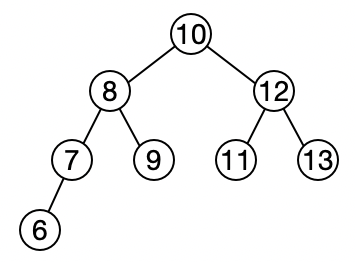
删除节点6或者节点7这种简单关系节点的话,直接删除就可以了。稍微麻烦的是,删除节点10这种,拥有左右子树的复杂关系节点。此时的删除操作分为两个步骤:
- 1)找出深度更大的一侧子树
- 2)用该侧子树中的最大(左子树)/最小(右子树)节点内容,替换被删除节点的内容
- 3)删除该侧子树中的最大(左子树)/最小(右子树)节点
- 4)检查平衡性
以删除节点10举例子:

- 1)step1:节点
10左子树深度为3,右子树深度为2,因此对深度更大的左子树进行操作。左子树中最大节点为节点9,使用节点9的内容,替换节点10的内容 - 2)step2:删除节点
9 - 3)step3:检查平衡性,发现左侧子树不平衡,通过旋转操作调整至平衡态
当然,删除操作也可以使用其他方式去做,不过这种使用最大/最小节点内容,替换被删除节点内容的方式,可以使得树结构的变化范围尽可能地小,所以相较而言效率也更好些。
3. 代码实现
AVL树的简单Python封装实现,已经开源上传至github并支持PyPI安装。但仅可作为简单场景使用及参考,实际应用需根据使用场景自行定制。