KMP算法的全称叫Knuth-Morris-Pratt算法,是一种比较常见的,基于前缀的,单字符串匹配算法。
对于这种算法,网上的各种解释介绍也很多,大多是从部分匹配表出发,来说明算法的构造使用方式,以及运行过程。所以咱们这一篇就不再重复介绍这部分了,而是从自动机的角度去介绍。
因此,在进行下面的章节之前,需要先阅读一下其他KMP算法的介绍文章,大致了解一下其构造、使用过程。其中比较清晰易懂的,可以参照阮一峰大神的这篇。
然后,具体的代码实现,可以直接跳转至最后一节,用以辅助理解。
1. 自动机?
部分匹配表的用法,是当匹配失败时,根据这张表里的跳转距离,把模式串的位置往后移动。而部分匹配表,又是根据模式串计算而来的。
例如上面那篇文章里的例子里,模式串ABCDABD对应的部分匹配表如下:
| A | B | C | D | A | B | D |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 2 | 0 |
而跳转距离公式是:移动位数 = 已匹配的字符数 - 对应的部分匹配值
所以,当匹配到下面位置时:
| A | B | C | D | A | B | X | A | B | C | D | A | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | D |
最后一个匹配的字符是B,其根据公式计算得到的跳转距离,就等于6 - 2 = 4,跳转后的位置,就变成了:
| A | B | C | D | A | B | X | A | B | C | D | A | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | D |
那么部分匹配表的值为什么是这样,跳转规则为什么要定?
先看一下部分匹配表的构造过程,其大致过程是寻找已匹配的部分串中,最长的,相同内容的前后缀。比如当已匹配部分是ABCDAB的时候,所有的前缀为[A, AB, ABC, ABCD, ABCDA],所有的后缀为[B, AB, DAB, CDAB, BCDAB]。其最长的,相同内容的前后缀就是AB,所以部分匹配值就等于2。
然后再看部分匹配表的使用,也就是跳转。当最后一个匹配的字符是B时,其跳转距离等于4。我们发现,跳转后,模式串中的前缀AB依然是匹配的。
结合这两部分,我们不难联想到Aho-Corasick算法中的失败路径。Aho-Corasick算法中,经过失败路径的跳转后,和KMP算法一样,我们的模式串依然保持着部分前缀的匹配。那么为了验证两者的关联性,我们为模式串ABCDABD建立Aho-Corasick自动机:
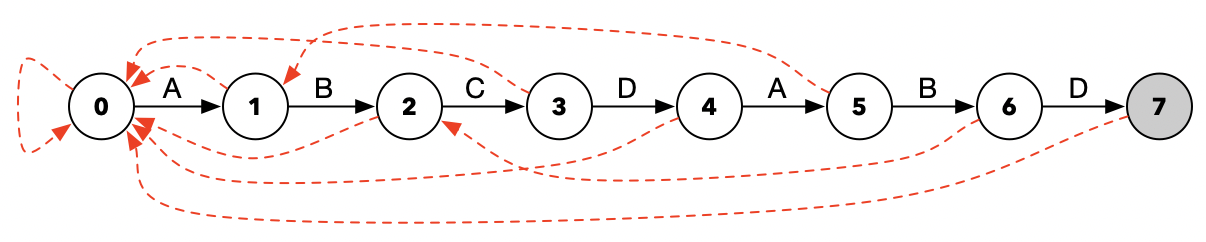
然后按照Aho-Corasick算法的跳转规则进行推算,发现每次跳转的距离,跟通过KMP算法计算得来的距离,和跳转后的匹配状态都是相同的。
所以,其实我们可以把KMP算法,看成是Aho-Corasick自动机的单模式串特殊情况。
2. 代码实现
KMP算法的Python封装实现,已经开源上传至github并支持PyPI安装。