算法学习之Aho-Corasick

Posted on

因为目前网上各处对于Aho-Corasick算法，在关键点上的解释都太简单随便，实在不如我意，所以在此用自己的语言记录一遍。

PS: 如果已经理解了该算法原理，或想要先拿到代码实现的话，请直接跳转至最后一节。

1. 什么是Aho-Corasick算法

Aho-Corasick又被简称为AC自动机，是一种基于前缀的，使用了确定有限自动机(DFA)原理的，字符串多模匹配算法。

2. 什么是DFA

DFA也就是确定有限自动机，英文全称是Deterministic Finite Automaton。具体的细节介绍，可以参照百度百科、维基百科，以及《算法导论》之类的算法书。在这里，我们尝试用通俗的语言和图示来解释一遍。

我们一个一个字母的来解释。首先，什么是自动机(A)。自动机就是一个代码块。这段代码块只做一件事，那就是接收输入值，和状态值，输出同为状态值的结果。用图示来表述，就是下面这样:

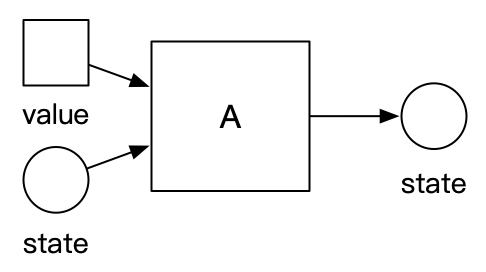
下一个字母——有限(F)，是指自动机接收、输入的状态种类是有限的。而相对应的，非有限自动机的状态就是有无限种的。

再下一个字母——确定的(D)，是指自动机的输出状态是单一的一个状态。如果不太好理解的话，那就是看一下对应的非确定自动机。这种自动机的输出状态，就不是单一的，而是许多个状态的集合。用图示来表述，就是下面这样:

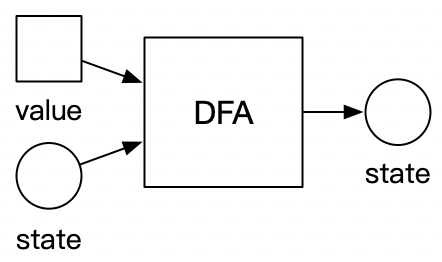
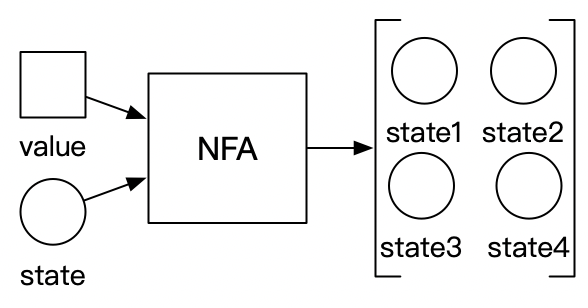
所以三个字母合起来以后，DFA的意思就像英文全称一样了，是一种状态值种类有限，且返回结果单一的自动机。举个简单的代码例子:

1
2
3
4
5
6
7
8
9
10
11
def automata(value, state):
	if state == 0:
		if value == 'a':
			return 0
		elif value == 'b':
			return 1
	elif state == 1:
		if value == 'a':
			return 0
		elif value == 'b':
			return 1

上面的这段代码，其内部的状态转化逻辑，可以用图示表示，也就是所谓的状态转化图:

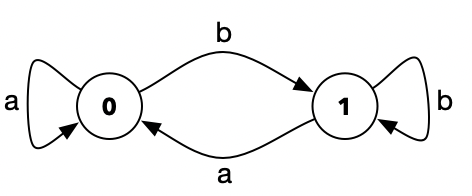
而更加复杂的自动机状态转化图，可以参照下面这张截取自百度百科的图示:

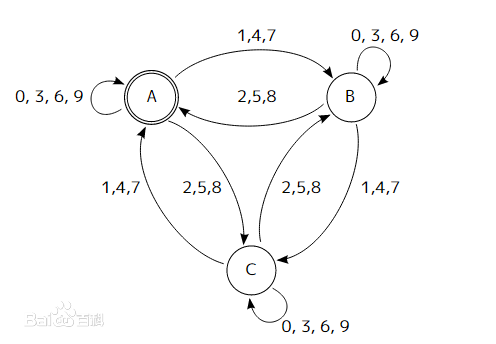
3. Tire Tree

上一节对DFA进行了介绍，那么现在实际操作一把，构建一个DFA状态转化图，使得输入下面三条字符串以后，都能得到终点态: aababbaba、aaabbaba、aabababa

我们先用纸笔画一画，会得到下面这样的状态转化图:

状态0为初始态，状态9为终点态。虽然可能不是十分完善，但我们输入上面那三条字符串的任意一条，都能成功的得到终点态9。那么既然能用纸笔画出来，我们就能用代码实现出来。大致构想一下代码的数据结构和逻辑，应该是下面这样:

  • 1) 首先，数据结构应该是使用链表来表示每个节点
  • 2) 其次，代码逻辑大致有下面这几步:
    • 2.1) 接收输入的字符，判断是否和当前状态所在节点的字符内容相同
    • 2.2) 如果不同，或者当前状态节点为初始态节点，则为本次输入字符新建节点。然后将当前状态所在节点的next指针，指向新建的节点
    • 2.3) 如果相同，则略过本次输入，跳转至步骤2.1接收下一个字符

我们按照这样的逻辑实现了以后，输入上面那三条字符串，会发现得到的结果，跟我们用纸笔画出的状态转化图不一样，而是像下面这样:

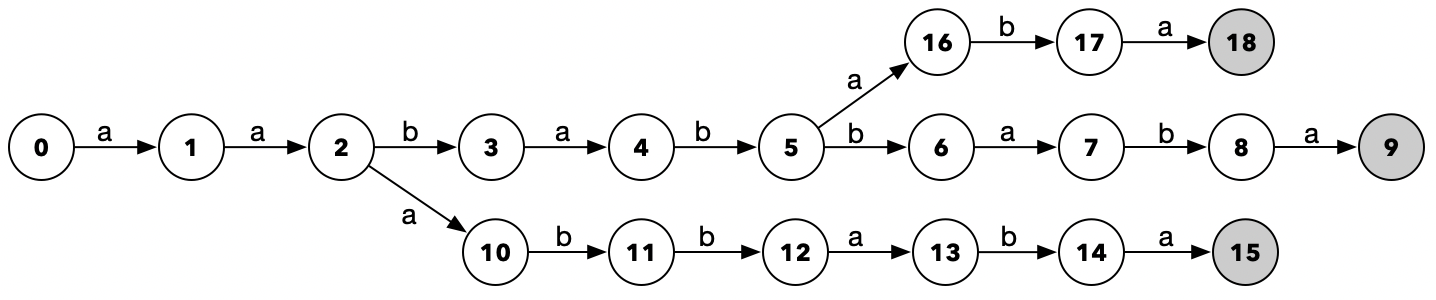
跟我们用纸笔画出来的图示，区别在于变成了树状的分叉结构。而这种我们无意之间得到的树状分叉结构，只要把状态节点，换成对应的输入字符内容，就是Tire Tree了，也叫做单词查找树。更加详细的介绍，可以参照算法书及各种百科和帖子。不过在这里，我们关注的重点是，Tire Tree和DFA的关系。

4. Aho-Corasick

按照上一节中生成Tire Tree类似结构DFA的代码设计，我们输入下面这三条字符串: his、hers、she。可以得到下面这样的状态转化图:

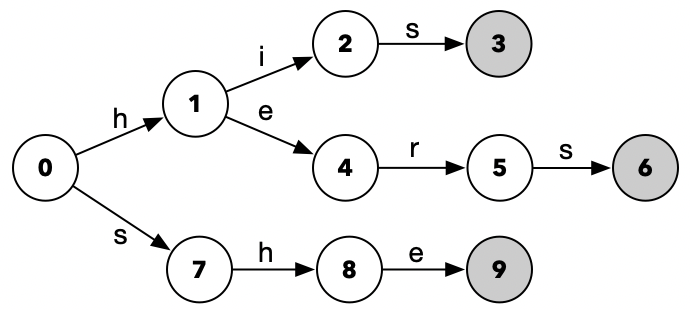
看着这个状态转化图，我们发现，或许可以拿来用做字符串匹配。比如我们输入这样一段内容: hisdef，当输入了s以后，我们就得到了终点态，所以我们可以判定当前字符串内包含有his。

可是，如果我们输入的是abchisdef呢？想要得到终点态，就得略过前面的abc。那如果我们输入的是shis呢？匹配she的时候匹配一半，就得切换到对his的匹配。因此，我们发现需要对这种状态树做一点改进。

在其他的帖子对Aho-Corasick算法的介绍里，都共同提到的一个重要点，就是想对于Tire Tree，Aho-Corasick算法多了一个Fail路径(失败路径)。还是用上面的his、hers、she做例子，添加了红色虚线Fail路径的状态转化图，像下面这样:

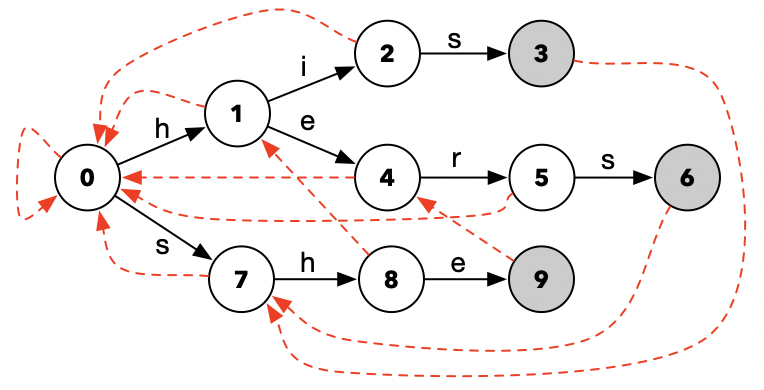
那这些红色的Fail路径的用法，就是如果我们输入的字符内容，无法使状态值，从当前状态节点，跳转到下一个预定的状态节点，我们就通过Fail路径，回溯到前面的某一个状态节点。举个例子，正常情况下的跳转动作是这样的: f(1, i) = 2。而当我们的输入值不是1和i的时候，就无法得到2了，得到的则是0，即f(1, x) = 0。

4.1 如何构建Fail路径

可是为什么要这样做呢？我们先看下该怎样构建Fail路径。同时，这一部分也是其他帖子里解释不够清晰的重要内容。总结为一句话，Fail路径，就是指向另一个，可以作为某一范式前缀的节点。其构建逻辑，可以分解成下面这几步:

  • 1) 如果自己是根节点，则指向自己
  • 2) 如果自己的父节点是根节点，则指向根节点
  • 3) 找到自己父节点Fail路径指向的节点，如果这个节点可以正常接收自己的输入字符，那么就指向这个节点接收自己输入字符后，所指向的那个节点
  • 4) 如果自己父节点Fail路径指向的节点不满足，就按照第3步的判断，检查自己父节点的父节点的Fail路径指向的节点
  • 5) 一直父节点、父节点、父节点这样的回溯，直到根节点还没找到的话，那么就指向根节点

我们按照上面说的步骤来，一步一步分析刚才his、hers、she例子得到的状态转化图。

  • 1) 首先是0节点，因为是根节点，所以就指向了它自己，也就是0 -> 0
  • 2) 然后是1节点，1节点的父节点是0节点也就是根节点，所以指向0节点，也就是1 -> 0
  • 3) 2节点的父节点是1节点，1节点的Fail路径指向了0节点。那么因为0节点，不能正常接收2节点的输入字符也就是i，所以我们继续回溯去看2节点的父节点的父节点，也就是0节点。这时，因为已经回溯到了根节点，所以按照逻辑，我们只能最终确定指向0，也就是2 -> 0
  • 4) 3节点的父节点是2节点，2节点的Fail路径指向了0节点。那么因为0节点，可以正常接收3节点的输入字符也就是h，所以3节点就应该指向，0节点接收了h后指向的节点，也就是6。所以最终，我们得到3 -> 6

后面其他节点的Fail路径，可以按照这样的逻辑一步步分析得到，所以就不啰嗦了。不过我们再提供另外一个例子，通过字符串nihao、hao、hs、hsr得到的状态转化图是下面这样:

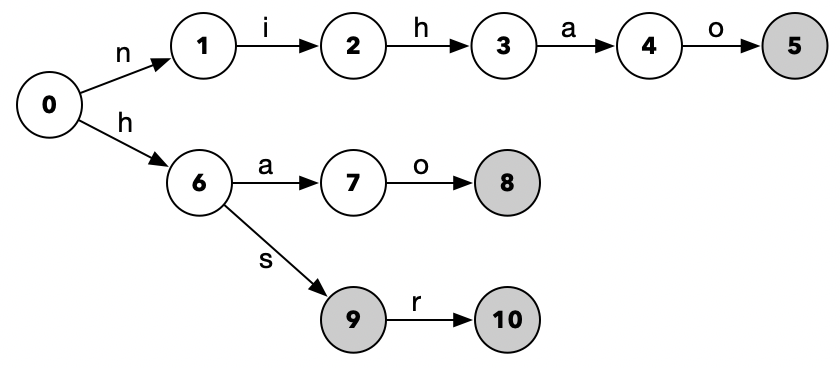
然后添上Fail路径:

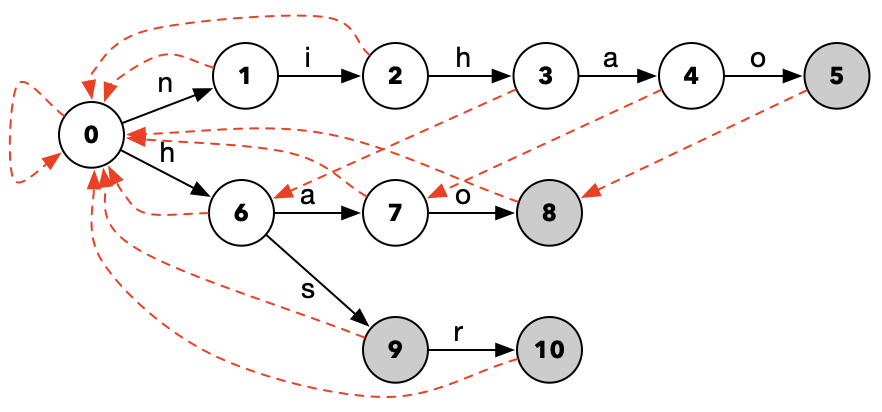
4.2 如何进行状态跳转

正常路径的跳转很简单，我们主要关注Fail路径的使用。和其文本含义一样，即当正常路径失败时，就通过Fail路径跳转。还是使用his、hers、she的状态转化图来举个例子，当我们输入ushhis时，详细的跳转步骤是下面这样的:

  • 1) 当前状态0，输入u，无法正常跳转，进入Fail路径，到达状态0
  • 2) 当前状态0，输入s，可以正常跳转，到达状态7
  • 3) 当前状态7，输入h，可以正常跳转，到达状态8
  • 4) 当前状态8，输入h，无法正常跳转，进入Fail路径，到达状态1
  • 5) 当前状态1，输入i，可以正常跳转，到达状态2
  • 6) 当前状态2，输入s，可以正常跳转，到达状态3

当我们执行到上面的第八步时，我们发现状态3是一个终点态。所以，我们可以判定，此时我们找到了范式his。

上面只是一个简单的例子，除此之外还有一些临界情况不太好处理，比如我们从一个终点态，通过Fail路径跳转到了另一个终点态。而这里，也同样是其他帖子里解释不够清晰的重要内容，所以我们详细的来介绍状态节点间的跳转逻辑:

  • 1) 如果当前这个节点，可以正常接收输入值，那么就跳转到输入值对应的下一个节点，本轮跳转结束，接收下一个输入值以进入下一轮跳转
  • 2) 如果当前这个节点，不能正常接收输入值，那么就先跳转到自己Fail路径指向的节点，然后再尝试执行第一步
  • 3) 如果现在已经跳转回到了根节点，那么先尝试第一步，如果失败，则就不再执行第二步，而是停留在根节点了，本轮跳转结束，接收下一个输入值以进入下一轮跳转

4.3 如何得到匹配结果

在上一节中，我们介绍了如何进行状态跳转，那如何得到匹配结果呢？

匹配结果由两部分组成:

  • 1) 每轮跳转结束后，所停留在的节点，如果是终点态，则该节点对应的模式串匹配成功
  • 2) 从停留的节点开始，一路沿Fail路径递归至根节点，期间路过的所有的节点，只要是终点态节点，则该节点对应的模式串也就匹配成功

用nihao、hao、hs、hsr的状态转化图举例。如果经过跳转后，停留在节点5，那么因为节点5是终点态，所以
节点5对应的模式串nihao就匹配成功了。然后我们沿着Fail路径递归至节点8，因为节点8也是终点态，所以节点8对应的模式串hao也匹配成功了。再继续沿着Fail路径递归，这时候我们到了根节点，那么至此，这一轮匹配结束。

4.4 Fail路径的意义

经过上面几节的介绍，我们已经知道了如何创建、使用Aho-Corasick算法实现，但我们一直不明白的是，Fail路径为什么这样构建，为什么能起作用。

为了解释这个问题，让我们回到本文最开始的位置。在第一节中，我们用一句话解释了什么是Aho-Corasick算法，而那句话中的“基于前缀的”这五个字，就是答案。

在我们使用Fail路径跳转的时候，我们发现，Fail路径所指向的节点，其所在的正常状态节点链上，从根节点开始，到该节点为止，每个节点组成的字符串，必定是某一个范式的前缀。

举个例子，由his、hers、she所组成的状态转化图里，节点9的Fail节点，指向了节点4。那么在节点4所在的这条状态节点链上，从根节点0开始，到节点4为止，一共0、1、4三个节点所组成的字符串是he，而he就是hers范式的前缀。

因此理解了为什Fail路径要这样指向以后，我们就弄懂了构建Fail路径的步骤。在构建Fail路径过程中，我们反复的回溯，其实就是在试图拓展上一步找到的前缀，而得到此范式的更长前缀。

5. 代码实现

Tire Tree和Aho-Corasick算法的Python封装实现，已经开源上传至github并支持PyPI安装。

地址点这里